무아레 무늬, 그래핀 격자 주기를 수십~수만 배까지 증폭
뒤틀림 각도에 따라 물성변화...절연체, 초전도체로 변신
고차-위상학적 절연...원래물질보다 두차원 경계낮은 금속성
“이중층 그래핀은 반드시 고차-위상학적 절연체여야”규명
뒤틀림 각도에 따라 물성변화...절연체, 초전도체로 변신
고차-위상학적 절연...원래물질보다 두차원 경계낮은 금속성
“이중층 그래핀은 반드시 고차-위상학적 절연체여야”규명
 이미지 확대보기
이미지 확대보기KAIST는 이 대학 이성빈 물리학과 교수팀이 두 겹으로 비스듬하게 겹쳐 있는 뒤틀린 이중 층 그래핀의 무아레 무늬(나노 물결 무늬)에서 새로운 고차-위상학적 양자 상태가 발생한다는 사실을 이론적으로 규명해 냈다고 4일 발표했다.
이 연구 결과는 뒤틀린 그래핀 이중 층 뿐 아니라 다양하고 복잡한 2차원 물질의 무아레 구조를 연구하는데도 적용할 수 있어 광범위한 응용이 가능할 것으로 기대된다. 특히 국내 물리학에서는 흔하지 않은 이론적 발견과 증명을 했다는 점에서 의미를 갖는다.
그래핀(graphene)은 탄소 원자 한 겹으로 이루어진 벌집격자 구조의 이차원 물질을 말한다. 무아레 무늬(moire pattern)는 그래핀 이중층을 뒤틀어서 겹쳐놓았을 때 각 층의 격자무늬 차이로 인해 나타나는 물결무늬를 일컫는다.
프랑스어로 ‘물결’이라는 뜻의 무아레(moiré)는 두 격자구조를 비스듬히 겹쳐 놓았을 때 물결이 일렁이듯이 나타나는 간섭무늬를 말한다. 모기장이 겹쳐 있는 부위에 햇빛이 비치면 물결무늬가 발생하는 것처럼 일상에서도 쉽게 확인할 수 있는 현상이다.
무아레 무늬는 일상생활뿐만 아니라 그래핀과 같은 이차원 나노 물질 두 겹을 비스듬하게 올려놓았을 때도 나타난다. 이때 뒤틀린 그래핀 이중 층에서 나타나는 무아레 무늬는 그래핀 격자의 주기를 수십에서 수만 배까지 증폭시킬 수 있다.
이러한 원리로 뒤틀림 각도에 따라 전기가 흐르지 않는 절연체가 되기도 하고 전기 저항이 아예 없는 초전도체가 되기도 하는 등 물성이 크게 변화할 수 있다. 특히 마법의 각도(magic angle)라고 불리는 1.1도 부근에서 전기 저항이 0이 되는 초전도 현상이 발견돼 이를 설명하기 위한 많은 연구가 진행 중이다.
고차-위상학적 절연체 상태는 새롭게 발견된 위상학적 절연체 중 하나이다. 기존 위상 절연체는 원래 물질보다 한 차원 낮은 경계면이 금속성을 띠는 특성을 갖지만, 고차-위상 절연체는 두 차원 낮은 경계가 금속성을 갖는다.
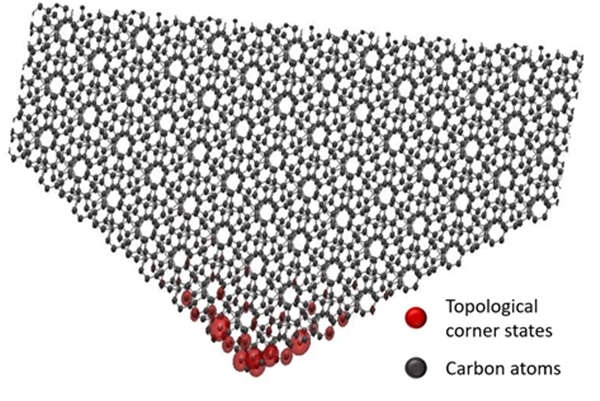
2차원 표면(surface) 물질을 예로 들면 위상 절연체의 경우 1차원 모서리(edge)에서 금속성을 확인할 수 있다면 고차-위상 절연체에서는 두 차원 낮은 0차원의 특정 끝부분(corner)에서 전자 상태가 된다.
이 2차원 물질 고차-위상학적 절연체의 존재는 아직 실험적으로 증명된 적이 없어 이 물질을 찾기 위한 연구들이 많은 관심을 받고 있다.
 이미지 확대보기
이미지 확대보기그러나 뒤틀린 그래핀 이중 층에서는 이러한 2차원 물질의 위상학적 양자 상태를 설명하기 위한 명확한 이론이 존재하지 않았다. 이는 뒤틀린 그래핀 이중 층에서 나타나는 무아레 무늬의 단위 격자당 탄소 원자의 개수가 수천에서 수만 개에 달해 전자의 움직임을 풀기에는 너무 복잡하기 때문이다.
이러한 탄소 기반의 전자 구조를 이론적으로 정확히 기술하기 위해서는 매우 큰 전산 능력의 대용량 컴퓨터를 이용하거나 특수한 상황으로 가정해 적용하는 근사방법들에 의존해야만 했다.
이 교수 팀은 문제해결을 위해 근사방법이 아닌 그래핀 이중 층의 무아레 무늬에서 나타나는 탄소 구조가 뒤틀림 각도에 상관없이 항상 일정한 몇 가지의 정확한 공간 대칭성을 가진다는 점을 이용했다. 이를 통해 뒤틀림 각도에 상관없이 이중 층 그래핀이 절연체라면, 이 이중 층 그래핀은 반드시 고차-위상학적 절연체 상태여야 한다는 사실을 이론적으로 규명했다.
이는 그래핀 이중 층이 가지는 회전 대칭성과 무아레 대칭 이동성이 뒤틀림 각도에 상관없이 항상 성립하는 것을 활용하는 원리이다. 연구팀의 이번 발견은 어떠한 근사방법에도 의존하지 않고 규명했다는 의의가 있다.
박문집 연구원이 1 저자로 참여한 이번 연구 결과는 국제 학술지 ‘피지컬 리뷰 레터스(Physical Review Letters)’ 11월 22일 자 온라인판에 편집자 추천(editors’ suggestion) 논문(논문명:‘Higher-Order Topological Insulator in Twisted Bilayer Graphene’)으로 선정됐다.
또한, 매달 전체 물리학계에서 중요하다고 여겨지는 주제를 소개하는 ‘네이처 리뷰 피직스 (Nature Review Physics)’ 연구 하이라이트(research highlight)에 11월 14일 자 ‘환상적 괴물’( Fantastic beasts)이란 제하의 기사로 소개되기도 했다.
 이미지 확대보기
이미지 확대보기박문집 연구원은 “격자구조의 대칭성만을 이용해 이중 층 그래핀의 위상학적 특성을 정확하게 이론적으로 기술했다는 의의가 있다”라며 “뒤틀린 그래핀 이중 층이 이차원 고차-위상학적 절연체의 새로운 후보가 될 수 있을 것이다”라고 말했다.
이번 연구는 KAIST 스타트업 펀딩, BK21, 한국연구재단의 지원을 받아 수행됐다.
그래핀의 발견과 함께 단일 원자 두께를 가지는 이차원 나노구조 물질들에 대한 연구가 폭발적으로 증가하고 있다. 최근 그래핀 분야의 가장 큰 관심사는 뒤틀린 이중층 그래핀으로써, 두 층간의 뒤틀림으로 인해 나타나는 무아레 격자 무늬가 전자 구조의 대칭 이동성을 수 십배에서 수 백 배 증폭시키는 현상이다.
무아레 대칭 이동성은 그래핀의 전자 구조를 매우 크게 변화시킬 수 있어 각도에 따른 이중층 그래핀의 전자 구조 변화를 설명하기 위한 이론연구들이 계속 되어오고 있다. 대부분의 기존 이론들은 매우 큰 전산 능력을 가진 대용량 컴퓨터를 이용하거나 뒤틀림 각도가 작은 경우에만 제한적으로 사용할 수 있는 근사방법들에 의존해야만 했다. 무아레 무늬의 전자구조들을 일반적으로 설명할 수 있는 통일된 전자구조이론을 기술하는 것은 매우 어려운 문제였다.
이성빈 교수 연구팀은 이중층 그래핀이 뒤틀림 각도에 상관없이 항상 일정한 몇가지 공간 대칭성을 가진다는 점을 이용하여 이중층 그래핀이 각도에 상관없이 일정한 고차-위상학적 상태를 가지고 있음을 이론적으로 규명했다. 이 방법은 이중층 그래핀의 무아레 구조가 가지는 특수한 반전대칭성 구조가 모든 각도에서 성립함을 응용한 것이다. 이 연구 결과는 어떠한 근사방법에 의존하지 않는다는 점에서 의의가 있다.
고차-위상학적 절연체 상태는 새롭게 발견된 위상학적 절연체의 한 종류로써 모서리에 국소화된 전자 상태에 의해 구별되는 새로운 물질군이다. 특히 이차원 물질 고차-위상학적 절연체의 존재는 아직 실험적으로 증명된 적이 없어 물질 후보를 찾는데 많은 연구가 진행되고 있다.
이 연구는 뒤틀린 이중층 그래핀의 통일된 위상학적 이론을 기술했다는 점, 또한 아직 실험적으로 발견되지 않은 고차-위상학적 절연체 상태를 예측함으로써 새로운 물질 후보를 발견했다는 점에서 의의가 있다. 본 연구는 뒤틀린 그래핀 이중층 뿐만 아니라 다양한 이차원 반 데르 발스 물질들의 무아레 구조를 연구하는데도 적용될 수 있어 광범위한 응용 가능성을 가질 것으로 기대된다.
이재구 글로벌이코노믹 기자 jklee@g-enews.com



























